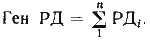|  |
phone: +7 495 1087345 fax: +7 495 1087345 office@trans-service.org |
RUSSIAN language only:
Navigation
Аналитическое счисление
Учет перемещения судна можно осуществлять не только графическими построениями на карте, но и путем выполнения расчетов по формулам аналитическим методом.
Аналитическое, или письменное, счисление применяется: при океанских переходах, когда отсутствуют крупномасштабные карты; при решении астрономических задач по определению места судна по Солнцу; во всех случаях, когда по какой-либо причине ведение графического счисления затруднено. Формулы аналитического счисления нашли широкое применение и во многих других вопросах навигации.
Сущность способа заключается в определении конечных координат судна по известным начальным координатам и их приращениям, рассчитанным по формулам
φ2 - φ1 = РШ
λ2 - λ1 = РД.
Выведем зависимость РШ и РД от истинного курса судна и плавания по нему.
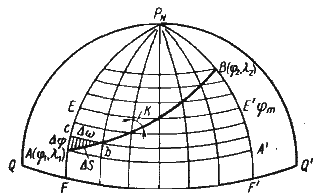
Предположим, судно совершило переход из пункта отхода A (φ1, λ1) в пункт прихода В(φ2, λ2) постоянным курсом К, пройдя расстояние S (рис. 57).
Разделим расстояние между пунктами A и B на большое число равных элементарных отрезков ΔS. Через полученные точки проведем меридианы и отрезки параллелей. В результате построения получим равные элементарные прямоугольные треугольники, которые по малости их можем рассматривать как плоские. Для удобства вывода формул Землю примем за шар.
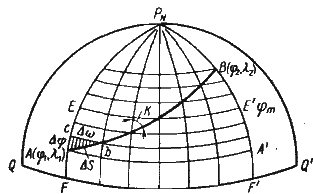
Рис. 57. К выводу формул аналитического счисления
Рассмотрим элементарный прямоугольный треугольник Abc. Гипотенуза тругольника Аb представляет собой отрезок локсодромии ΔS. Катет Aс является отрезком меридиана и представляет собой элементарную разность широт Δφ. Катет cb представляет собой элементарное расстояние по параллели между меридианами точек А и b, называемое элементарным отшест-вием Aw.
На основании формул плоской тригонометрии из треугольника Abc можно выразить катет Ас: Δф = ΔS cos К.
Перейдя к бесконечно малым величинам, напишем дифференциальное уравнение
dφ = dS cos К.
Проинтегрируем данное уравнение с учетом того, что К — величина постоянная
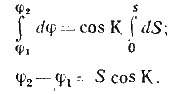
или в окончательном виде
РШ=S cos K. (79)
В этой формуле РШ получается в морских милях, но так как 1 морская миля равна 1' дуги меридиана, то, следовательно, и РШ можно считать выраженной в угловых минутах.
Катет be из треугольника Abe выразим:
Δw= ΔS sin К.
Перейдем к бесконечно малым величинам и проинтегрируем полученное дифференциальное уравнение
dw=dS sin К.
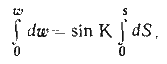
w=SsinK или ОТШ=SsinK. (80)
Для расчета долготы точки прихода нам необходимо получить значение РД. Из элементарного треугольника Abe можем написать
Δwi/ Δφ = tg К.
Выразим длину элементарного отшествия через элементарный отрезок дуги экватора Δλ: Δw = Δλcosφ и подставим его в приведенное выше выражение
Δλ cosφ/Δφ = tg к.
отсюда
Δλ= tg KΔφ/cosφ.
Перейдем к бесконечно малым величинам и проинтегрируем полученное дифференциальное уравнение
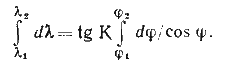
Это выражение нам ужезнакомо (см. § 17), следовательно,
λ2 — λ1 = (D2-D1)tgK
или
PД = РМЧ tgK. (81)
Формула (81) широко используется в навигации. Однако для расчета долготы конечной точки необходима формула, связывающая отшествие с разностью долгот.
Напишем ряд равенств, выражающих длины элементарных отрезков дуг экватора через элементарные отшествия:
Δλ1 = Δw sec (φ1 + Δφ);
Δλ2 = Δw sec (φ1 + 2Δφ);
Δλ3 = Δw sec (φ1 + 3Δφ);
Δλm = Δw sec (φ1 + mΔφ) = Δw sec φ2.
Просуммировав обе части равенств, получим
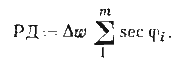
Правую часть равенстваумножим и разделим на т
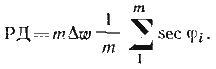
Произведение тΔw = ОТШ, т.е. представляет собой отшествие, а выражение — средний арифметический секанс, который соответствует вполне определенной широте, называемой промежуточной широтой φп. После подстановки получим
РД=ОТШsecφi. (82)
Формула (82) точная, но не удобна для применения, так как необходимо знать φп.
После деления формулы (80) на формулу (79) получим
tgK=OTШ/PШ.
Полученное выражение tgK подставим в формулу (81). В результате будем иметь
РД = ОТШ х РМЧ/РШ. (83)
Эта формула так же относится к числу точных формул. Сравнивая выражения РД (82) и (83), можно сделать вывод
sec φп = РМЧ/РШ или
φп=аrc sec РМЧ/РШ. (84)
Следовательно, ОТШ представляет собой расстояние между меридианами начальной и конечной точек в милях по промежуточной параллели, широта которой определяется выражением (84).
При плавании на короткие расстояние можно считать, что в интервале широт от φ1 до φ2 sec изменяется линейно и, следовательно,
φп≈(φ1 + φ2)/2 = φm
Тогда формула (82) примет вид
РД =OTШ sec φm. (85)
Формула является приближенной.
По формулам (79) и (80) составлена таблица 24 «Разность широт и отшествие» в МТ — 75. Аргументами для входа в таблицу служат ИК и плавание S, выбираются — РШ и ОТШ.
Таблица 25а МТ — 75 составлена по формуле (85) и служит для выбора разности долгот по отшествию и средней широте. Аналитическое счисление подразделяется на простое, составное и сложное
Если судно совершает плавание из одного пункта в другой одним курсом, то аналитическое счисление будет простым. В этом случае рассчитываются по формулам (79), (80) и (85) или выбираются из таблиц 24 и 25а РШ и РД. Координаты пункта прихода определяются: φ2 = φ1 + РШ; λ2 = λ1 + РД.
Если при переходе из одного пункта в другой судно совершает плавание несколькими курсами и при этом координаты конечного пункта рассчитываются через генеральную разность широт и генеральное отшествие, то аналитическое счисление называется составным.
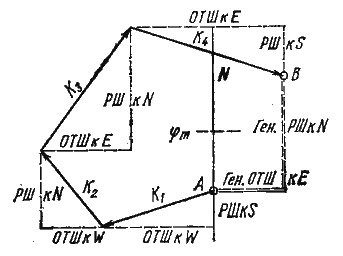
Последовательность действий в этом случае такова: рассчитав по формулам или выбрав из таблиц для каждого курса РШ и ОТШ со своими знаками, находят их алгебраические суммы, которые называются генеральной разностью широт (Ген РШ) и генеральным отшествием (Ген ОТШ) (рис. 58). При этом необходимо иметь в виду, что знак отшествия определяется следующим образом: если составляющая движения судна по параллели направлена к востоку, то знак отшествия «+», и наоборот « — ».
Расчеты ведутся по формулам
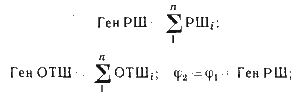
φm = (φi+φa)/2; РД = Ген ОТШ sec φm;
λ2 = λ1 + РД
Если при плавании учитывается дрейф судна от ветра, то в формулы (79) и (80) вместо ИК надо подставлять ПУα. Это же касается и использования таблицы 24 МТ — 75.
Если же в районе плавания действует постоянное течение, то его учитывают как еще один дополнительный курс. При этом за курс принимается направление течения, а за плавание — снос течением ST за время его действия t, т.е.
ST = vT t.
Формулы аналитического счисления
позволяют не только находить
координаты конечного пункта, но и решать различные другие задачи.
|
|
|
|
Рис. 58. К расчетам составного аналитического счисления |
Рис. 59. К расчетам простого аналитического счисления |
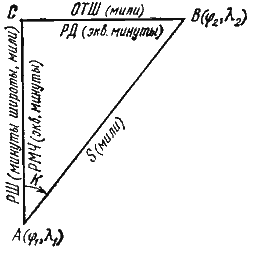
Так, зная координаты начального и конечного пунктов, можно вычислить расстояние между ними и курс для перехода в конечный пункт. Формулы легко можно вывести из треугольника ABC (рис. 59)
| S = РШ sec К |
(86) |
| S = OTШ cosec K | (87) |
| tg К = РД/РМЧ |
(88) |
При плавании в высоких широтах для получения более точных результатов используют сложное аналитическое счисление.
В отличие от составного счисления, при сложном счислении не используют Ген ОТШ. В этом случае определяют генеральную разность долгот (Ген РД) как алгебраическую сумму РД на каждом курсе, т.е.