 |  |
тел.: +7 495 1087345 факс.: +7 495 1087345 office@trans-service.org |
Навигация
Картографические проекции
Для обеспечения безопасности судовождения необходимо постоянно знать положение судна относительно ближайших навигационных опасностей и траектории избранного маршрута перехода.
Следовательно, на судне необходимо иметь изображение земной поверхности с нанесенными на ней очертаниями берегов и деталями рельефа дна.
Наиболее наглядное и точное изображение с сохранением подобия изображаемых объектов и соотношения их площадей дает глобус.
Однако от его использования отказались, так как даже при недостаточной навигационной информации он имеет недопустимо большие габариты. Кроме того, вести учет плавания судна на сферической поверхности намного сложнее, чем на плоскости.
Поэтому в практике мореплавания с древних времен было принято изображать участки земной поверхности на плоскости, т.е. использовать карты.
Наука, занимающаяся составлением, производством и использованием карт, называется картографией.
Развернуть сферическую поверхность Земли в плоскость без разрывов и складок невозможно. Поэтому приходится прибегать к растяжениям и сжатиям, что приводит к искажениям изображаемых участков.
Математически выраженный способ изображения поверхности земного эллипсоида или шара на плоскости называется картографической проекцией.
Суть всякой картографической проекции определяется функциональной зависимостью между географическими координатами точки на Земле и ее же координатами на проекции:
x=f1(φ; λ), y= f2(φ2; λ)
Другими словами, можно сказать, что картографическая проекция — это способ условного изображения на плоскости совокупности координатных линий, называемой картографической сеткой.
Общим требованием для всех картографических проекций является непрерывность и однозначность функциональных зависимостей географических и картографических координат точек. В этом случае изображение земной поверхности будет сплошным, без разрывов.
Картографические проекции по характеру искажений делятся на следующие классы:
- равноугольные или конформные;
- равновеликие или эквивалентные;
- произвольные.
Равноугольные проекции сохраняют равенство углов между какими-либо направлениями на карте углам между теми же направлениями на местности. В этих проекциях сохраняется подобие фигур, а частный масштаб в любой точке одинаков по всем направлениям.
Равновеликие проекции сохраняют пропорциональность между площадями фигур на карте и на местности.
К произвольным проекциям относят все остальные, которые не удовлетворяют условиям равноугольности и равновеликости.
Кроме того, картографические проекции делятся по способу построения картографической сетки. Из числа этих проекций кратко рассмотрим только азимутальные, конические и цилиндрические.Азимутальная проекция (рис. 26) получается проектированием по тому или иному закону сетки географических меридианов и параллелей на плоскость, касательную к поверхности Земли в какой-либо точке.
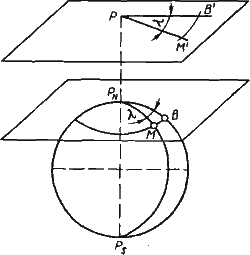
Рис. 26. Азимутальная проекция
Если за точку касания этой плоскости принять один из географических полюсов Земли, то получим параллели в виде концентрических кругов, а меридианы в виде радиальных линий, исходящих из точки касания.
Коническая проекция (рис. 27) получается проектированием сетки географических меридианов и параллелей на поверхность конуса, касающегося или рассекающего поверхность Земли, с последующим развертыванием конуса в плоскость. В этой проекции меридианы изображаются прямыми, исходящими
из одной точки, а параллели — концентрическими окружностями с общим центром в этой же точке. Многие географические карты выполнены в этой проекции.
Цилиндрическая проекция получается проектированием сетки географических меридианов и параллелей на поверхность цилиндра, касающегося по большому кругу или секущего по малым кругам поверхность Земли. В этом случае меридианы и параллели на проекции представляют собой взаимно перпендикулярные прямые линии.
Уравнение цилиндрических проекций имеет следующий вид:
x=f(φ); y=cλ (57)
где х — удаление заданной параллели от экватора;
φ — широта заданной параллели;
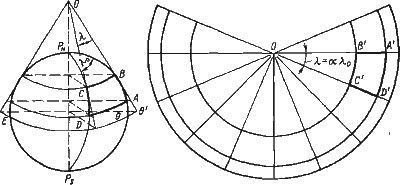
Рис. 27. Коническая проекция
у — расстояние между начальным и заданным меридианами по экватору;
с — коэффициент пропорциональности;
λ — долгота заданного меридиана.
Если ось Земли и ось цилиндра совпадают, то проекция называется нормальной цилиндрической (рис. 28).
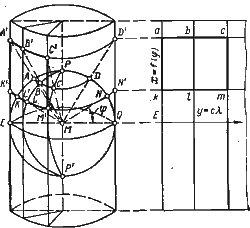
Рис. 28. Нормальная цилиндрическая проекция
В этой проекции все меридианы и параллели изображаются прямыми параллельными линиями, причем меридианы и параллели взаимно перпендикулярны. Нормальная цилиндрическая проекция может обладать свойствами равноуголь-ности, равновеликости или быть произвольной в зависимости от избранного закона проектирования. Равноугольная нормальная цилиндрическая проекция является основной для построения морских карт. Если ось цилиндра лежит в плоскости экватора Земли, то проекцию называют поперечной цилиндрической.
Равноугольная поперечная цилиндрическая проекция является основной для построения многих речных карт и атласов.
При использовании любой картографической проекции земная поверхность на карте изображается в уменьшенном виде. Степень уменьшения отрезков на карте относительно соответствующих отрезков на местности называется масштабом.
Так как нет картографических проекций, свободных от искажений, то масштаб карты является величиной переменной. Он меняется с изменением направления и с переходом от одной точки к другой.
Поэтому масштабом карты в какой-либо точке по заданному направлению называется отношение бесконечно малого отрезка на карте к соответствующему бесконечно малому отрезку на местности, т.е.
C=dS0/dS,
где dS0 — бесконечно малый отрезок на карте в данной точке по заданному направлению;
dS — бесконечно малый отрезок на местности, соответствующий отрезку на карте.
Этот масштаб называется частным масштабом карты.
При составлении карты используются так называемый главный масштаб, который сохраняет свое постоянство по определенной линии (например, параллели), называемой главной, или в определенных точках карты.
Масштаб может выражаться в виде дроби, числитель которой — единица, а знаменатель — число, показывающее степень уменьшения изображения на карте. Такой масштаб называется числовым или численным. Например, числовой масштаб 1/250000 означает, что единице длины на карте соответствуют 250 тыс. таких же единиц длины на местности. Этот масштаб может быть записан и в таком виде: 1 : 250000 или 0,000004.
Иногда удобнее для измерения отрезков использовать линейный масштаб. Линейным масштабом называется величина, показывающая, сколько единиц длины высшего порядка (миль, км и т. д.) на местности содержится в единице длины низшего порядка (см, мм) на карте.
Обычно принято линейный масштаб на картах изображать в виде горизонтальной шкалы. Он может быть задан в виде: в 1 см — 5 морских миль.
Принято считать, что длину какого-либо отрезка на карте можно измерить с точностью до 0,2 мм.
Линейное расстояние на местности, соответствующее 0,2 мм на карте, называется предельной точностью масштаба. Так, предельная точность масштаба 1/300000 равна 60 м.







