Меркаторская проекция

Большинство МНК составляется в нормальной равноугольной цилиндрической проекции Меркатора. На ней линия пути (локсодромия) изображается в виде прямой и отсутствует искажение углов. Эти свойства максимально упрощают графическое решение задач на карте.

Уравнения проекции имеют вид:

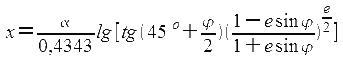
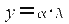
где: α – постоянная величина (параметр проекции), е – эксцентриситет земного эллипсоида.

С помощью уравнений проекции по заданным географическим координатам точки на эллипсоиде или шаре, можно вычислить плоские прямоугольные координаты этой точки на карте.

При расчетах картографической сетки и графических построениях на карте используется меридиональная часть (МЧ или D):

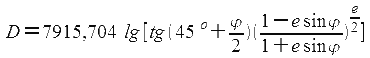
В этой формуле параметр α приравнен к радиусу экватора в минутах дуги экватора (а=3437,747').

МЧ это расстояние по меридиану от экватора до данной параллели в нормальной равноугольной цилиндрической проекции Меркатора, выраженное в экваториальных минутах при масштабе на экваторе равном единице. Значение меридиональных частей можно выбрать по широте из таблицы 26 МТ-75. Для N полушария МЧ имеют знак «+», а для S - «-». Отрезок меридиана на меркаторской проекции, выраженный в экваториальных минутах определяется разностью меридиональных частей (РМЧ или ΔD) крайних точек отрезка.

Геометрическая интерпретация построения меркаторской проекции.

Если землю принять за шар, то уравнения меркаторской проекции и формула МЧ принимает вид:

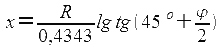
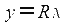
( в качестве главной параллели служит экватор)

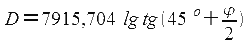
Меркаторская проекция равноугольная, поэтому масштаб в каждой точке карты по всем направлениям одинаков, однако величина его изменяется в зависимости от широты, а вдоль каждой параллели он постоянен.

Для нахождения частного масштаба используют модуль параллели. Модулем параллели называется коэффициент на который надо умножить главный масштаб чтобы получить частный масштаб, т. е.:

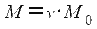
Он определяется по формуле:

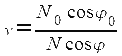
где N – радиус сечения первого вертикала.

Если в качестве главной параллели взять экватор (N₀=a, cos 0°=1), то модуль параллели:

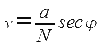
а частный масштаб:

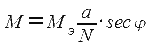
Так как отношение a/N изменяется в незначительных пределах (1...0,997), можно сделать вывод что, практически, масштаб изменяется пропорционально secφ:

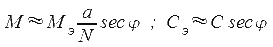
Следовательно на картах вблизи экватора частный масштаб мало отличается от главного и изменяется медленно. В высоких широтах он, с удалением от главной параллели, изменется быстро. Поэтому на картах в нормальной проекции в высоких широтах очень большие искажения площадей и использование проекции становится невозможным. Это видно из выражения:

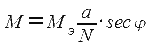
при φ=90° M=∞.

Знаменатель экваториального масштаба С_Э можно выбрать по заданному главному масштабу из таблицы 33 МТ-75.

На горизонтальных сторонах рамки карты в нормальной проекции Меркатора разбивается шкала долгот в минутах. Так как меридианы на карте параллельны между собой, то длины одной минуты всех параллелей, в том числе и экватора, на карте одинаковы, поэтому изображение одной минуты параллели е используют в качестве единицы длины при различных графических построениях; е – называется единица карты и как длина одной минуты экватора равна:

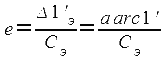
где Δ1'_Э – длина одной минуты экватора.

Длину одной минуты параллели на карте е можно рассчитать по формуле:

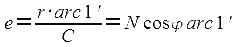
где r – радиус параллели с широтой φ; С – знаменатель частного масштаба в широте φ.

Таким образом единицей карты называется длина изображения одной минуты параллели на карте в меркаторской проекции. Обычно ее выражают в миллиметрах.

При расчете длины отрезка S_n любой параллели на карте, ограниченного меридианами с долготами λ₁ и λ₂ используется формула:

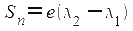
Для расчета отрезка любого меридиана на карте следует единицу карты умножить на РМУ концов отрезка D₁ и D₂:

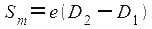
Вертикальные, боковые, стороны рамки карты, являются шкалой широты.

Длина изображения одной минуты меридиана на карте в нормальной меркаторской проекции называется меркаторской милей. Меркаторская миля δ выражается в миллиметрах и рассчитывается по формуле:

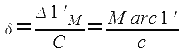
где Δ1'_М -длина одной минуты дуги меридиана земного эллипсоида; М – радиус кривизны меридиана. Заменяя числитель значением Δ1'_М по формуле:

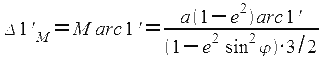
и, выражая δ в миллиметрах, получим:

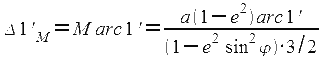
Последняя формула показывает, что длина меркаторской мили увеличивается с увеличением широты. Поэтому при измерении длин на карте необходимо пользоваться шкалой вертикальной стороны рамки в том диапазоне широт, в котором находится измеряемый отрезок.

Но и в этом случае при измерении расстояний по вертикальной стороне рамки карты допускается методическая погрешность, вызванная тем что, переменная длина одной минуты дуги меридиана на карте (меркаторская миля) принимается постоянной, равной одной морской миле т. е. 1852 м. Эта погрешность равна:

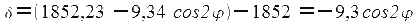
Следовательно, если на Земле измерено расстояние S в морских милях, то на карте следует отложить S_K меркаторских миль:

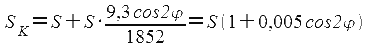
Таким образом:

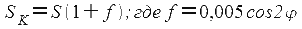
Величину f, умноженную на 100, можно выбрать из таблицы 25 МТ-75.

Если требуется, снятое с карты расстояние S_K в меркаторских милях перевести в морские мили то используется формула:

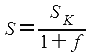
Анализ выражения S_K=S(1+f) показывает, что значение коэффициента f не превышает ±0,005S (+ на экваторе; - на полюсах), а в средних широтах f≈0. Поэтому учет поправки за различие в длине изобоажения на карте морской и меркаторской мили целесообразен только в экваториальной и приполюсных зонах при измерении расстояний в несколько десятков миль.