Ошибки наблюдений и точность обсерваций

Измерения навигационных параметров так же, как и любые наблюдения, сопровождаются ошибками. Причинами возникновения этих ошибок являются несовершенство используемых для наблюдений приборов и инструментов, влияние внешней среды, недостатки принятого способа измерений, а также ограниченные возможности органов чувств и восприятий человека.

Для оценки точности обсерваций в навигации пользуются выводами теории ошибок. Согласно этой теории все ошибки подразделяются на случайные, систематические и промахи.

Случайные ошибки — это ошибки наблюдений, причины возникновения которых неизвестны, а их индивидуальные значения не подчинены какой-либо закономерности, в данном ряду наблюдений их величины и знаки могут непрерывно меняться. Свойства этих ошибок проявляются только при большом числе измерений одной и той же величины, в одинаковых условиях и с одинаковой точностью.

Мерой оценки точности при действии случайных ошибок принята средняя квадратичная ошибка ±m. Вероятность того, что при измерении ошибка будет находиться в пределах средней квадратичной, составляет 68,3%.

Часто для оценки точности измерений используют так называемую предельную ошибку, которая равна ±3m. Вероятность такой ошибки 99,7%. Однако в штурманской практике используется предельная ошибка, равная ±2m с вероятностью 95,4%.

Наиболее просто значение средней квадратичной ошибки может быть рассчитано по методу размаха. Для этого рассчитывают размах R как разность абсолютных значений наибольшего и наименьшего результатов из выполненной серии измерений.

Значение средней квадратичной ошибки одного измерения получают по формуле

m = R/K.

где К — коэффициент, который выбирается по числу измерений в серии п. Соответственно он равен для n : 5 — 2,32; 6 — 2,53; 7 — 2,70; 8 — 2,85; 9 — 2,97; 10 — 3,08; 11 — 3,16.

Из свойств случайных ошибок можно сделать следующий практический вывод: для уменьшения влияния случайных ошибок необходимо выполнить серию из 3 — 5 измерений навигационного параметра и результаты осреднить.

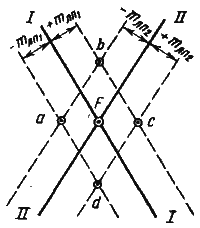
Рис. 65. К действию случайных ошибок

Систематические ошибки — ошибки, которые остаются постоянными в данной серии измерений или изменяются по определенному закону при изменении условий наблюдений. В большинстве случаев систематические ошибки могут быть определены и в виде поправок приборов и инструментов внесены в результаты измерений.

Систематические ошибки, зависящие от несовершенства инструмента, называются инструментальными.

Кроме того, установлено, что разные наблюдатели производят измерения неодинаково. Подобные систематические ошибки, зависящие от индивидуальных свойств наблюдателя, называются личными ошибками наблюдателя.

Чаще всего систематические ошибки действуют на результат наблюдений в одном направлении, т.е. имеют определенный знак, а поэтому не могут быть обнаружены и исключены из наблюдений многократными измерениями. По этой причине судоводитель должен всегда уделять большое внимание выверке приборов и инструментов и тщательному определению их поправок.

Промахами называются грубые ошибки, превышающие по абсолютной величине пределы точности для данного вида наблюдений и являющиеся следствием невнимательности и небрежности наблюдателя. Промах может быть обнаружен повторными наблюдениями или вычислениями и их контролем.

На практике для выявления промахов часто прибегают к расчету предельной ошибки. Если в ряду измерений имеются ошибки, превосходящие по своей величине предельные, то они исключаются как промахи, так как вероятность их появления менее 0,3%.

В реальных условиях систематические и случайные ошибки действуют всегда совместо, и, складываясь алгебраически, образуют полную ошибку.

Определение места судна сводится к построению на карте двух или более линий положения, которые связаны определенной зависимостью с измеренными навигационными параметрами. Изменение величины навигационного параметра, равное ΔU, приводит к тому, что линия положения на карте сдвигается параллельно себе на величину, называемую смещением Δn.

Если вместо приращения навигационного параметра ΔU рассматривать ошибку его измерения m_v, то смещение будет представлять собой ошибку линии положения m_лп.

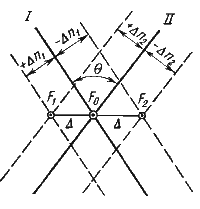
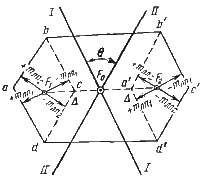
При определении места судна по измерению двух навигационных параметров в результате действия случайных ошибок обе линии положения окажутся смещенными параллельно себе на величины ±m_лш1 и ±m_лп2. Вероятность смещения в ту или иную сторону одинакова. Поэтому на рис. 65 построены линии, соответствующие смещению +m_лш1, +m_лп2 и — m_лш1, — m_лп2. Пересечение крайних смещенных линий положения дает нам теперь не точку, а фигуру погрешности в виде параллелограмма abcd, площадь которого будет характеризовать точность места судна. Если для построения фигуры погрешности приняты средние квадратичные ошибки в измерении навигационных параметров m_v1 и m_v2, то вероятность нахождения места судна в ее пределах будет менее 50%.

Если принять предельные ошибки измерения навигационных параметров ±2m_v1 ±2m_v2 или ±3m_v1, ±3m_v2, то вероятность повысится соответственно до 91 и 99%.

Часто при оценке точности места судна удобнее оперировать не площадью вероятного местонахождения его, а числом, характеризующим эту точность. Для этого используют формулу, выражающую точность определения  места  М₀,   полученного  по  двум  линиям  положения:

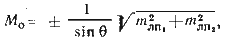 (8)

где m_лп1 , m_лп2    — средние квадратичные ошибки первой и второй линий положения; θ — угол пересечения линий положения.

Средняя квадратичная ошибка определения места по двум линиям положения М₀ представляет собой радиус круга, в пределах которого вероятность нахождения места судна равна 63,2 — 68,3%.

Анализ формулы показывает, что, помимо всего прочего, точность определения места зависит от угла пересечения линий положения θ. Чем ближе угол θ к 90°, тем точность определения места выше.

Как видно из изложенного, для оценки точности определения места судна графическим построением или расчетами по формуле (89) необходимо знать зависимость величины смещения (ошибки) линии положения от ошибки в измерении навигационного параметра.

Эту зависимость принято выражать с помощью градиента навигационного параметра.

В общем случае градиентом функции называется ее изменение на единицу расстояния по нормали в сторону возрастающих значений функции. Следовательно, градиент навигационного параметра g, являясь вектором, определяет изменение величины навигационного параметра при смещении линии положения  на одну единицу длины.

Математическое выражение модуля градиента имеет вид:

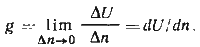 (90)

Направлен градиент по нормали к линии положения в сторону увеличения значения навигационного параметра. На основании формулы (90) можем написать

Δn=ΔU/g  (91)

или, переходя к ошибкам,

m_лп = m_U/g.  (92)

Задаваясь значением ошибки измерения навигационного параметра m_U и зная для него выражение градиента, можно рассчитать ошибку линии положения m_лп.

Для оценки точности обсервации на практике поступают так. Проведя пересекающиеся линии положения на карте (см. рис. 65), определяют их ошибки ±m_лп1 и ±m_лп2 в зависимости от случайных ошибок в измерении навигационных параметров. При этом, если ошибки измерения навигационных параметров невозможно рассчитать из наблюдений, то ими задаются исходя из опыта плавания в подобных условиях. Далее, откладывают по нормали от линий положения в обе стороны, соответствующие ±m_лп1 и ±m_лп2. Через полученные точки проводят прямые, параллельные линиям положения. Пересечение этих прямых образует фигуру вероятного нахождения места судна abсd.

Влияние систематических ошибок на место судна проявляется по-иному. В этом случае обе линии положения сместятся в одну сторону и величина их смещения может быть определена по формуле (91).

Рассчитав значения Δn₁ и Δn₂, выполняют такое же построение, как и при случайных ошибках, так как знак систематической ошибки неизвестен. В результате построения получают не площадь вероятного местонахождения судна, а линейное смещение обсервованной точки Δ = F₀F₁ = F₀F₂ (рис. 66).

При совместном действии случайных и систематических ошибок систематическая ошибка смещает место судна на величину Д, в ту или иную сторону в зависимости от ее знака, а случайные ошибки образуют площадь вероятного местонахождения судна около этих точек. Суммарная площадь будет образована ломаной линией, охватывающей площади вероятного местонахождения судна при различных знаках систематической ошибки (рис. 67).