Учет течения

Горизонтальные перемещения водных масс в морях и океанах на­зываются морскими течениями.

К элементам, характеризующим течение, относятся направление К_т и скорость v_т. Направление течения определяется в градусах по той точке горизонта, куда оно направлено («течение идет из компаса»). Скорость течения измеряется в узлах.

По характеру изменения элементов течений принята следующая их навигационная классификация:

• постоянные течения;
• периодические течения;
• временные течения.

Постоянные течения вызываются длительно действующими причинами и характеризуются тем, что их направления и скорости значительное время остаются постоянными. Причинами возникновения таких течений могут служить, например, постоянно дующие ветры.

Периодические течения вызываются действием периодических сил и характеризуются непрерывным изменением своих элементов, периодически повторяющих их прежние значения. К ним относятся приливно-отливные течения, вызываемые действием периодических приливообразующих сил Луны и Солнца.

Временные течения вызываются различными преходящими факторами: действием ветра, дующего продолжительное время в одном направлении; изменением плотности воды из-за большого испарения ее или притока пресной воды. Такие течения наиболее трудно поддаются учету.

Наличие морских течений в значительной степени усложняет счисление пути судна.

Под действием гребных винтов судно перемещается относительно воды по направлению истинного курса. Это перемещение фиксируется лагом. Одновременно вся масса воды перемещается по направлению и со скоростью действующего течения, увлекая с собой движущееся судно. Это перемещение относительными лагами отмечено не будет. Следовательно, судно будет участвовать в двух движениях: в движении относительно воды со скоростью V_л (или V_об) по направлению истинного курса; в движении вместе с массой воды со скоростью и по направлению течения.

Таким образом, особенность плавания судна при действии течения заключается в том, что: перемещение его происходит по направлению суммарного вектора скоростей; диаметральная плоскость при движе­нии сохраняет направление, параллельное истинному курсу; относи­тельный лаг не учитывает перемещения, вызванного течением.

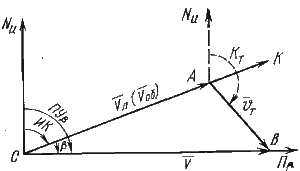
Для сложения векторов на карте от исходной точки С (рис. 45) прокладывают по направлению истинного курса вектор относительной скорости судна V_л, из конца которого А в том же масштабе проводят вектор течения v_т. Отрезок прямой СВ, соединяющий исходную точ­ку с концом вектора течения, даст направление и величину суммарного

вектора скорости судна V относительно дна (вектор абсолютной ско­рости).

Линия, по которой перемещается центр массы судна относительно дна, обусловленная влиянием течения, называется линией пути на течении.

Угол, заключенный между северной частью истинного меридиана и линией пути на течении, отсчитываемый в круговой системе счета, называется путевым углом на течении ПУ_β (ПУ_Т).

Угол, заключенный между линией истинного курса и линией пути на течении, называется углом сноса β.

Истинный курс и путевой угол на течении связаны между собой следующими формулами:

ПУ_β = ИК+β; (68)

ИК = ПУ_β — β; (69)

β = ПУ_β — ИК. (70) 

Формулы алгебраические, так как угол сноса входит в них со своим знаком. Если течение сносит судно вправо, т.е. линия пути располагается правее линии истинного курса, то β имеет знак плюс.

При учете течения также приходится решать прямую и обратную задачи.

Прямая задача. В этом случае по известным ИК, относительной скорости судна и элементам течения необходимо определить β, ПУ_β и V.

Графические построения, выполняемые при решении прямой задачи, которые сводятся к определению направления и величины вектора абсолютной скорости судна, рассмотрены нами на примере (см. рис. 45).

Таким образом, графическое решение формулы (68) позволяет определить направление пути судна и его абсолютную скорость.

Треугольник CAB принято называть скоростным, так как все его стороны представляют собой векторы скоростей.

Необходимо иметь в виду, что изменение любого вектора скоростного треугольника влечет за собой изменение других векторов, кроме v_т.

При построении треугольника в зависимости от масштаба карты длину всех векторов можно одновременно увеличить или уменьшить в несколько раз (например, взять не скорости, а расстояния за 2 ч или 30 мин и т.п.).

Решение обратной задачи. В этом случае по известным ПУ_β, скорости судна и элементам течения необходимо определить β ИК и V.

На карте от исходной точки С прокладывают линию пути судна и вектор течения CD (рис. 46). Из конца вектора течения D радиусом, равным относительной скорости судна, проводят циркулем отрезок ду­ги окружности так, чтобы он пересек линию пути (точка В). С помощью параллельной линейки направление DB переносят в исходную точку, так как оно соответствует направлению линии ИК судна.

Указанным графическим построением решается формула (69). Для определения величины и знака угла сноса β используют формулу (70).

Длина отрезка линии пути СВ представляет собой в масштабе карты абсолютную скорость судна.

Данные о течениях помещаются в специальных атласах и таблицах течений, в лоциях и на морских навигационных картах. Часто судо­водителю приходится определять элементы течения по обсервациям.

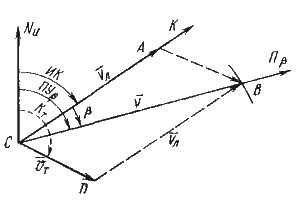Рис. 45. К нахождению линии Пβ	Рис. 46. К нахождению линии ИК

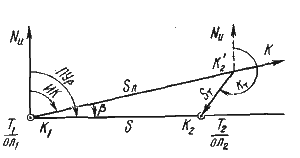
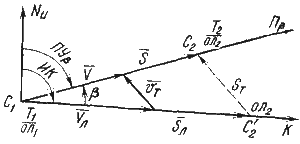
Рис. 47. Определение элементов течения по обсервациям	Рис. 48. Нахождение счислимой точки на линии Пβ

Пусть судно в момент Т₁, ол₁ находилось в обсервованной точке K₁, и следовало по линии ИК с постоянной скоростью (рис. 47). В момент T₂, ол₂ вновь определили место судна по береговым ориентирам и рассчитали его счислимое место. Под действием собственных движителей судно, пройдя отрезок К₁К'₂ = S_Л, должно было находиться в точке К₂'. Полученная при отсутствии ветра в момент T₂ невязка К'₂К₂ является следствием действия неизвестного течения и представляет собой снос за время (Т₂ — Т₁).

Направление течения определяется по направлению невязки К₂'К₂, а его скорость рассчитывается по формуле

v_T=K'₂K₂/(T₂-T₁)

Рассмотрим решения основных навигационных задач, так как при учете течения они имеют свои особенности.

Нахождение счислимой точки на линии пути. По разности отсчетов лага для начальной и искомой точки определяют по формуле (50) пройденное расстояние, которое откладывают в масштабе карты по линии ИК (рис. 48). Полученную точку С'₂ сносят но направлению течения на линию пути судна. Искомое счислимое место судна будет находиться на линии пути в точке С₂. У точки С'₂ указывается отсчет лага, а у точки С₂ — дробью в числителе — время, в знаменателе — отсчет лага.

Треугольник С₁С'₂С₂ получил название путевого или навигацион­ного, так как все три стороны характеризуют плавание судна: С₁С'₂ — плавание по направлению ИК под действием, движителей (S_Л); С'₂С₂ — снос судна течением (S_T); С₁С₂ — плавание по линии пути (S).

При графическом счислении на карте показываются как линия истинного курса, так и линия пути судна.

В случае попутного или встречного течения угол сноса равен соответственно 0 или 180°. Абсолютная скорость судна и пройденное расстояние рассчитываются:

V=V _л + v_т; S = S_л + S_T — при попутном течении;

V=V_л — v_т; S = S_л — S_T — при встречном течении, где S_Л — определяется по формуле (50),

a S_T = (T₂ — T₁)v_т.

Расчет времени и отсчета лага прихода судна в заданную точку. Предположим, что необходимо рассчитать время Т₂ и отсчет лага ол₂ прибытия судна в точку С₂ (рис. 49). Для этого переносят заданную точку по направлению, обратному вектору течения, на линию ИК- 

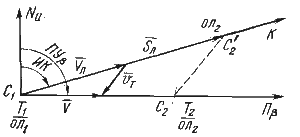
Рис. 49. Расчеты прибытия в заданную на линии П_β точку

Полученный отрезок С₁С'₂ представляет собой в масштабе карты расстояние пройденное судном по лагу.

Зная S_л, К_л, V_л, расчеты Т₂ и ол₂ выполняют так, как указано в § 22.

Частным случаем этой задачи является расчет Т₂ и ол₂ прихода судна на траверз какого-либо ориентира. В этом случае рассчитывают траверзный истинный пеленг по формуле (67).

Место судна в момент траверза С₂ будет находиться в пересечении линии пути судна и проведенной от ориентира М линии траверзного пеленга (рис. 50).

Далее действия и расчеты выполняют аналогично предыдущей задаче.

Учет приливно-отливных течений. Особенность приливноотливных течений заключается в том, что их направления и скорости меняются как с течением времени, так и с изменением места. Учитывать такие течения известными нам приемами невозможно. Поэтому приливно-отливные течения рассматривают за короткий промежуток времени (обычно за 1 ч) как постоянные, имеющие осредненные значения их элементов.

В этих условиях прямая и обратная задачи по учету течения решаются в той же последовательности, как мы рассматривали ранее. Данные по приливно-отливным течениям помещаются в специальных атласах, таблицах или на морских навигационных картах.

Для определения осредненных элементов течения рассчитывают время Т₁ прибытия в точку начала его учета. По координатам этой точки и времени Т₁ из соответствующего пособия выбирают элементы течения. Далее находят счислимые координаты судна на время Т₂ = Т₁+1 ч.

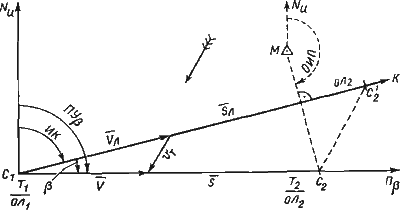
Рис, 50. Расчеты прихода на траверз ориентира

Вновь выбирают из пособия, но уже по новым координатам и времени Т₂ элементы течения для второй точки.

Осреднив найденные элементы приливно-отливного течения, учи­тывают его в период плавания с Т₁ до Т₂ как постоянное течение. Такие расчеты выполняют для каждого часа плавания.

Точность счисления при учете приливно-отливных течений понижается, поэтому необходимо чаще контролировать место судна по обсервациям.