|  |
тел.: +7 495 1087345 факс.: +7 495 1087345 office@trans-service.org |
Навигация
Совместный учет течения и дрейфа судна
В практике судовождения довольно часто встречаются случаи, когда одновременно с учетом дрейфа судна от ветра приходится учитывать и снос течением.
Чтобы не ошибаться в последовательности действия при совместном учете течения и дрейфа, необходимо помнить, что в скоростном треугольнике одна из сторон всегда представляет собой вектор относительной скорости судна. В данном случае этот вектор направлен по линии пути при дрейфе. Рассмотрим решение прямой и обратной задач.
Прямая задача. Содержание ее заключается в том, что по известным ИК, относительной скорости (по лагу или частоте вращения), углу дрейфа и элементам течения необходимо определить путевой угол ПУС и абсолютную скорость судна.
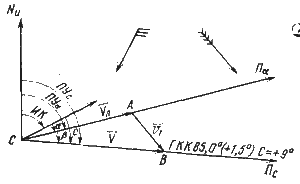
Исходя из ранее изложенной рекомендации определяют направление вектора относительной скорости судна по формуле (62). От точки начала совместного учета течения и дрейфа С проводят линию Пα и откладывают на ней длину вектора относительной скорости судна (рис. 51). Из конца этого вектора А прокладывают вектор скорости течения. Соединив начальную точку С с концом вектора течения В, получают линию пути судна.
Угол, заключенный между линией пути судна при дрейфе и линией пути, будет являться углом сноса судна течением β
Угол, заключенный между линией истинного курса и линией пути судна, называется углом суммарного сноса с.
Величина и знак угла суммарного сноса определяются алгебраической суммой
с =α + β. (71)
Путевой угол судна будет получен из выражения
ПУс=ИК + с. (72)
Значение абсолютной скорости находят измерением длины отрезка СВ.
При ведении графической прокладки на карте проводят от исходной точки линию Пα и линию Пс. Линию истинного курса показывают коротким (3 — 4 см) отрезком, чтобы дать представление о положении диаметральной плоскости судна.
Счисление ведется таким же образом, как и при учете одного течения, только пройденное расстояние по лагу (по частоте вращения) откладывается не по линии истинного курса, а по линии Пα.
Обратная задача. В этом случае по известным ПУС, относительной скорости (по лагу или частоте вращения), углу дрейфа и элементам течения определяют ИК судна и его абсолютную скорость.
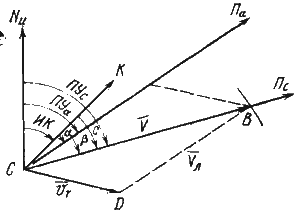
От исходной точки С прокладывают линию избранного пути и вектор течения (рис. 52). Из конца вектора течения D, как из центра, радиусом, равным относительной скорости судна, проводят дугу окружности так, чтобы она пересекала линию Пс (точка В).
Направление отрезка DB, соответствующее направлению Пα, переносят в исходную точку С.
Величину и знак угла сноса от течения определяют из выражения
β = ПУс-ПУα. (73)
Определив по формуле (71) суммарный снос, рассчитывают значение истинного курса
ИК = ПУС — с. (74)
Абсолютная скорость судна находится из скоростного треугольника измерением длины отрезка СВ в масштабе карты.
Совместный учет течения и дрейфа судна может дать хорошие результаты лишь в случае точного знания элементов течения, угла дрейфа и изменения скорости судна под влиянием ветра и волнения. Такие возможности в практике плавания встречаются нечасто. Поэтому возникает необходимость в определении пути судна другими способами. Наиболее достоверно он определяется по ряду обсерваций, но для этого в видимости судоводителя должно находиться одновременно несколько ориентиров.
Ориентиром для определения пути судна может служить любой неподвижный предмет, даже не обозначенный на карте. Способы применимы лишь в том случае, если за весь период наблюдений действующие в районе плавания факторы сноса судна остаются неизменными.
Определение пути судна по трем пеленгам одного ориентира и времени.
|
|
|
|
Рис. 51. Определение линии пути при учете суммарного сноса |
Рис. 52. Определение ИК при учете суммарного сноса |
|
|
|
|
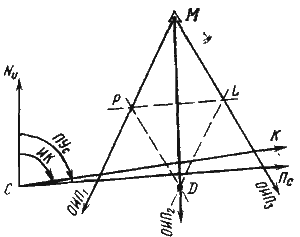
Рис. 53. Определение пути (частный случай)
|
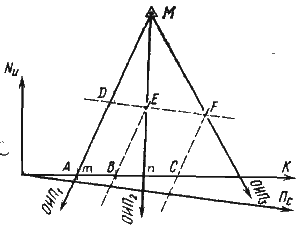
Рис. 54. Определение пути (общий случай) |
Частный случай способа. Следуя постоянным курсом и скоростью, измеряют через равные промежутки времени три компасных пеленга ориентира М (рис. 53). Интервалы времени между пеленгованиями ориентира выдерживают с высокой точностью по секундомеру. Следовательно, расстояния, проходимые судном за эти промежутки времени, будут равны.
После исправления пеленгов поправкой компаса их обратные направления прокладываются от ориентира М.
Задача сводится к построению такой прямой линии, на которой пеленги отсекали бы равные между собой отрезки. В этом случае направление прямой будет параллельно искомой линии пути судна.
Наиболее простой прием построения заключается в следующем. Через произвольную точку среднего пеленга ОИП2 (например D) проводят прямые линии, параллельные крайним пеленгам, до пересечения с ними в точках Р и L.
Направление прямой, соединяющей точки Р и L,будет параллельно линии пути судна, так как отсекаемые пеленгами отрезки будут равны между собой. С помощью параллельной линейки направление пути судна переносится в счислимую точку.
Общий случай способа. Сохраняя постоянство курса и скорости, измеряют три пеленга на ориентир М через произвольные промежутки времени (рис. 54). Моменты пеленгования T1, Т2 и Т3 замечают с высокой точностью по секундомеру. Следовательно, расстояния, проходимые судном между пеленгами, будут пропорциональны промежуткам времени ΔT1= Т2 — T1 и ΔТ2 = Т3 — Т2. После исправления пеленгов поправкой компаса их обратные направления проводят от ориентира М.
Задача по определению линии пути судна сводится к построению такой прямой линии, на которой пеленги отсекли бы отрезки m и n, пропорциональные ΔT1 и ΔТ2. Поступают следующим образом. Рассчитывают отрезки
m = kΔT1 , n = kΔT2,
где k — произвольно выбранный коэффициент пропорциональности, которым может быть и скорость судна.
Далее откладывают по линии ИК (счислимого пути) от точки А пересечения ее с первым пеленгом два смежных отрезка АВ = т. и ВС = n.
Через точки В и С проводят линии, параллельные первому пеленгу, до их пересечения со вторым и третьим пеленгом (точки Е и F).
Прямая DF, проведенная через точки £ и F, будет удовлетворять условию
DE/EF=т/п = ΔT1ΔT2
Следовательно, она параллельна линии пути судна. Назначение коэффициента пропорциональности k легко можно понять, если учесть, что графическое построение может выполняться не от ориентира, а от произвольной точки на свободном месте карты или же на обычном листе бумаги.
Если в условиях действия постоянного течения и ветра в качестве ориентира использовать свободно плавающую вешку с малой парусностью, то в результате наблюдений будет определено направление пути судна при дрейфе.
Объясняется это тем, что течение сносит в равной степени и судно, и вешку, в то время как ветер воздействует только на судно.
Способ симметричных наблюдений. Применяется в том случае, если планируется проходить траверз ориентира, до которого можно измерить расстояние или его вертикальный угол. При этом ориентир может быть не нанесен на карту, а его высота неизвестна судоводителю. Сущность способа заключается в следующем. В точке А на остром курсовом угле ориентира М (рис. 55) измеряют пеленг на него, а также расстояние или его вертикальный угол. После прохода траверза ориентира, в момент когда расстояние до него или его вертикальный угол вновь станут равными первым наблюдениям, измеряют второй пеленг на ориентир.
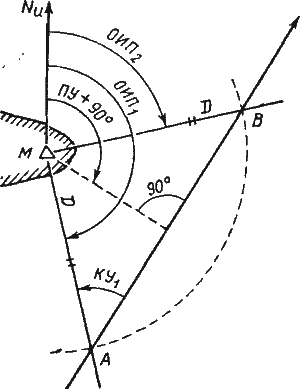
Рис. 55. Определение пути по симметричным наблюдениям
Исходя из условий наших наблюдений можно утверждать, что полученный треугольник АВМ является равнобедренным, а его основание АВ соответствует направлению фактического перемещения судна, т. е. линии пути. Значение ПУ может быть определено из треугольника АВМ по элементарной формуле
ПУ = (ИП1, + ИП2)/2 ± 90°.
Рассмотренные способы позволяют определить в зависимости от действующих на судно внешних факторов угол дрейфа, угол сноса течением или угол суммарного сноса.
Точность графического счисления с учетом внешних факторов. В § 22 был рассмотрен вопрос точности графического счисления в зависимости от ошибок в показаниях курсопоказателей и лагов.
Однако на точность счислимого места судна значительное влияние оказывают ошибки в учете течения и дрейфа. Результатом действия всех указанных факторов является возникновение векторальных ошибок, которые складываются квадратически, так как имеют случайный характер:
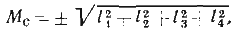
где Мс — радиус круговой ошибки (круга погрешности);
l 1, l2, l3, l 4 — векториальные ошибки.
Рассмотрим значения
векториальных ошибок: l 1 — результат действия ошибки в пути при дрейфе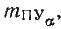 по аналогии
с выводом в § 22 можем написать
по аналогии
с выводом в § 22 можем написать
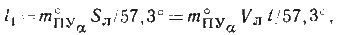
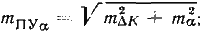
где
тΔк — ошибка в поправке компаса, для гирокомпаса может составить ±1,0°;
т — ошибка в учете угла дрейфа, может достигать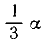 ;
;
/2
— результат действия ошибки в поправке лага
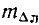 ,
,
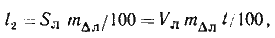
где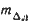 —
у хорошо выверенного лага принимается в пределах
2 — 3 %;
—
у хорошо выверенного лага принимается в пределах
2 — 3 %;
/3 — результат действия ошибки в направлении
учитываемого течения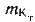
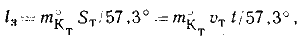
где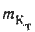 —
в хорошо изученных районах принимается равной 20 — 30°;
—
в хорошо изученных районах принимается равной 20 — 30°;
/4
— результат ошибки в скорости учитываемого течения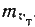 ,
,
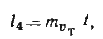
где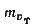 —
принимается равнойскорости
—
принимается равнойскорости
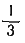 выбираемого из пособия течения.
выбираемого из пособия течения.
После подстановки значений векториальных ошибок получим формулу радиальной (круговой) ошибки счисления
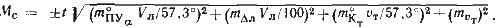 (75)
(75)
Данная формула находит практическое применение в том, что на ее основании делают вывод о возможности дальнейшего плавания по счислению.
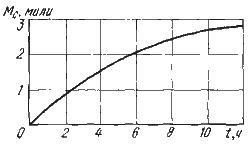
Рис. 56. Зависимость точности счисления от продолжительности плавания
При плавании несколькими курсами ошибка счисления в конце последнего курса будет определяться выражением:
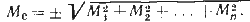 (76)
(76)
где М1, М2, ..., Мn — ошибки счисления на каждом курсе.
Недостатком данного способа является то, что выполняемые расчеты базируются на субъективных оценках случайных ошибок в элементах, характеризующих движение судна.
В настоящее время широко используется статистический способ оценки точности счисления, основанный на выводах теории случайных функций. Он позволяет более объективно учесть влияние внешних факторов (действие ветра и течения) и неточность в работе приборов.
В соответствии с выводами этой теории ошибка счисления за первые 2 — 3 ч плавания подчинена линейному закону, т.е. увеличивается прямо пропорционально продолжительности плавания. В дальнейшем она растет пропорционально квадратному корню из продолжительности плавания, т.е. по параболическому закону.
Если на основании данных систематического плавания в одном и том же районе составить график зависимости ошибки счисления Мс от продолжительности плавания судна без обсерваций t, то полученная кривая (рис. 56) подтвердит эти выводы.
Для расчета средней квадратичной радиальной ошибки счисления используют формулы:
|
|
(78) |
где Кс — коэффициент точности счисления, который характеризует нарастание радиальной средней квадратичной ошибки счисления по времени.
Коэффициент точности счисления рассчитывается по невязкам Сi которые выбираются из судового журнала. Используя их, составляют ряд уравнений:
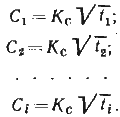
Для получения нормальных уравнений обе части равенств умножают на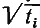
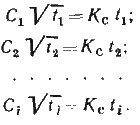
После суммирования решают полученное уравнение относительно
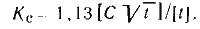
Коэффициент 1,13 введен в формулу, чтобы результат был получен с вероятностью 68,3%.